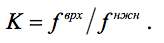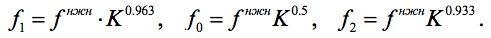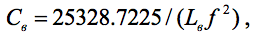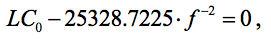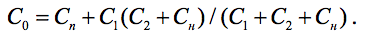Что-то не так?
Пожалуйста, отключите Adblock.
Портал QRZ.RU существует только за счет рекламы, поэтому мы были бы Вам благодарны если Вы внесете сайт в список исключений. Мы стараемся размещать только релевантную рекламу, которая будет интересна не только рекламодателям, но и нашим читателям. Отключив Adblock, вы поможете не только нам, но и себе. Спасибо.
Как добавить наш сайт в исключения AdBlock
QRZ.RU > Каталог схем и документации > Схемы наших читателей > Радиолюбительские конструкции > Об одном варианте расчете сопряжения гетеродинного контура (Oscillator Padding)
Реклама
Об одном варианте расчете сопряжения гетеродинного контура (Oscillator Padding)
В радиолюбительской практике при построении супергетеродинных радиоприёмников определённые трудности вызывает настройка сопряжения входного и гетеродинного контуров преобразовательного каскада. Если диапазон принимаемых частот сильно растянут (невелик т.н. коэффициент диапазона), бывает достаточно обеспечить сопряжение контуров в одной точке, при большем перекрытии требуется сопряжение в 2-х точках диапазона, в общем же случае необходимо добиться сопряжения в 3-х точках. Для этого приходится подбирать опытным путём или рассчитывать 3 сильно взаимосвязанных параметра для каждого контура – индуктивность и ёмкости пары конденсаторов растяжки диапазона. В данной статье описывается новый вариант решения данной задачи – методом наименьших квадратов (МНК), применённым к системе трёх нелинейных уравнений с тремя неизвестными. Приводится описание соответствующей ЭВМ-программы, опубликованной автором в сети Интернет для свободного пользования.
I. Суть метода
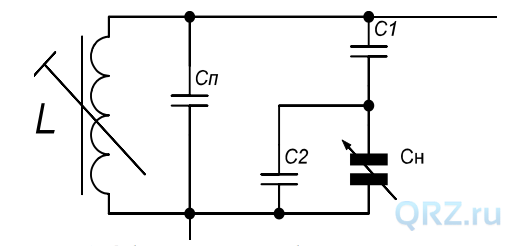
Пусть имеется 2 колебательных контура – входной (УВЧ, смесителя) (Вместо понятия входной контур, контур УВЧ и т.п. в специальной литературе часто используется термин контур переселектора; здесь отдаётся предпочтение первому варианту, т.к. под переселектором обычно имеется в виду не только входной контур как таковой, но и усилительный каскад, и даже несколько таковых; вообще же речь может идти и о единичном входном контуре без всякого усилителя, суть задачи от этого не меняется) и гетеродинный, в состав каждого из которых входит катушка индуктивности, L; ёмкость монтажа суммарно с собственной ёмкостью катушки, Cп; конденсатор настройки Сн и два конденсатора растяжки диапазона, С1 и С2 (см. рис.1).
Рис.1. Общая схема колебательного контура.
1о. Исходные данные:
- Lв – индуктивность входного контура, мкГн,
- ёмкости Сп обоих контуров,
- минимальная и максимальная ёмкости конденсатора настройки (конденсатора переменной ёмкости, КПЕ) - Cнmin , Cнmax (для обоих контуров одинаковые),
- граничные частоты диапазона входного контура: fвниж , fвврх , мГц
- частоты точного сопряжения гетеродинного контура в этом диапазоне (три точки): f1-нижняя, f0-средняя, f2-верхняя,мГц,
- кроме того, заданы: промежуточная частота преобразования, fпр , мГц и тип настройки гетеродина (нижняя или верхняя настройка).
2о. Требуется найти (вычислить):
1) ёмкости С1в , С2в конденсаторов растяжки входного контура (1-ый этап расчёта);
2) ёмкости С1г , С2г конденсаторов растяжки и индуктивность Lг гетеродинного контура (2-й этап).
Алгоритм решения данной задачи, в общем, сводится к следующему (см., например, ссылки [1, 2]).
Сначала задаётся независимо либо вычисляется индуктивность входного контура. Если задана полная ёмкость входного контура на какой-либо границе диапазона, то по частоте и ёмкости находится индуктивность. Затем вычисляется полная ёмкость входного контура на другой границе диапазона. Отсюда алгебраически находятся ёмкости конденсаторов растяжки входного контура. Далее находятся значения ёмкости конденсатора настройки (КПЕ) в трёх точках сопряжения диапазона, частоты которых также должны быть заданы; очевидно, что эти же значения ёмкости КПЕ будут таковыми же и для гетеродинного контура. Переносятся частоты сопряжения на контур гетеродина, путём добавления к ним или вычитания из них значения промежуточной частоты.
Формулируется уравнение для частоты колебательного контура, куда входят 3 неизвестных параметра: Lг , С1г , С2г . Таковые вычисляются путём совместного решения данного уравнения в 3-х точках (для 3-х частот) сопряжения гетеродинного контура. В литературе описан порядок расчёта алгебраическим способом [2], однако обоснование алгоритма не приводится. В сети Интернет на радиолюбительских форумах можно встретить ссылки на программу в Excel [3], которая, по-видимому, реализует именно этот алгоритм, но, к сожалению, использование программы не представляется удобопонятным. Ниже постановка и детали задачи рассматриваются подробно. Отличие состоит в том, что на конечном этапе решение находится нелинейным методом наименьших квадратов (МНК), что при наличии соответствующей программы для ЭВМ у пользователя, даже не имеющего представления о методе, не должно вызывать ни трудностей ни временных затрат.
II. Основное уравнение для частоты колебательного контура
Как известно, частота колебательного контура связана с ёго индуктивностью и ёмкостью соотношением:
где частота задаётся в герцах, индуктивность - в генри, а ёмкость - в фарадах. Если частоту выражать в мГц, индуктивность в мкГн, а ёмкость в пФ, то формула принимает вид:
Полная ёмкость контура, изображённого на рис.1, задаётся формулой:
В дальнейшем при нахождении величин индуктивности и ёмкостей конденсаторов растяжки гетеродинного контура по МНК уравнение (1) приводится к более линейному виду:
III. Расчёт ёмкостей конденсаторов растяжки входного контура
Зная границы диапазона входного контура fвниж , fвврх и задав желаемую полную ёмкость его, C0 , на одной из границ диапазона, целесообразно сначала найти его индуктивность
Впрочем значение Lв может быть задано независимо из иных соображений, например, имеется готовая катушка подходящей индуктивности.
Затем по индуктивности и частоте другой границы диапазона вычисляется полная ёмкость входного контура на 2-й границе. Обозначим т.о. полученные величины через C0min и C0max . Верхние индексы будем относить к высокочастотной и низкочастотной границам диапазона, соответственно.
Применим формулу (2) к границам диапазона входного контура, получив т.о. 2 уравнения для расчёта емкостей С1,С2 (индекс «в» для краткости опускаем):
Приведём эти уравнения к виду
и разделим второе на первое, чтобы исключить C1 . Получим уравнение с одним неизвестным C2 :
Вводя вспомогательные величины
и приводя к общему знаменателю, перепишем его в виде
Раскрываем скобки и приводим подобные члены, получаем квадратное уравнение для нахождения C2:
Теперь можно найти C1 :
Когда ёмкости конденсаторов растяжки известны, легко найти ёмкость конденсатора настройки в любой точке диапазона, зная полную ёмкость контура на
заданной частоте:
На этом первый этап решения задачи заканчивается. Нам известны все необходимые параметры входного контура. По ним необходимо определить соответствующие параметры контура гетеродина.
IV. Определение точек сопряжения контуров
Коэффициент диапазона контура есть величина, показывающая степень покрытия частот при изменении ёмкости конденсатора настройки от Снmin до Снmax :
Считается [1, 2], что добиваться сопряжения контуров по трёхточечной схеме необходимо, когда K > 1.7 ; если эта величина лежит в диапазоне от 1.1 до 1.7, то достаточно 2-х точек сопряжения, а если она меньше 1.1, то достаточно одной точки. Для трёхточечной схемы частоты сопряжения задаются соотношениями:
Следующей целью является нахождение ёмкости конденсатора настройки на
данных частотах входного контура. Сначала по индуктивности Lв и частотам сопряжения вычисляются значения полной ёмкости входного контура в трёх точках:
а затем по формуле (5) – три значения ёмкости конденсатора настройки. Перенос частот (6) на контур гетеродина осуществляется путём добавления или вычитания промежуточной частоты. В итоге имеем следующий набор данных для вычисления 3-х параметров гетеродинного контура: три значения частоты, три значения ёмкости конденсатора настройки. Дальнейшие действия сводятся к отысканию параметров L, C1 и C2 уравнения,
где
Поскольку искомые величины должны удовлетворять данным соотношениям с максимальной точностью, то для решения задачи годится МНК в отношении минимизации отклонений функции (8) от нулевых значений. В нашем случае используется нелинейный МНК в варианте Гаусса-Зайделя (т.н. метод линеаризации модели) с введением гасящих множителей. Описывать его здесь не имеется возможности, поэтому сразу перейдём к описанию пользовательского интерфейса готовой программы решения обоих этапов рассматриваемой задачи.
V. Программная часть
Программа написана на языке Basic в среде VBA (Visual Basic for Applications). Это встроенный язык программирования Excel в пакете MS Office [4]. Для того, чтобы пользоваться программой, необходимо, чтобы на ПК, оснащённом ОС MS Windows XP или более поздней, было установлено приложение MS Office Excel.
Проделать следующее:
- Скачать и сохранить файл программы oscillator_padding_3pointfit.xls, пройдя по ссылке [5].
- Открыть приложение Excel, не открывая скачанного файла.
- Т.к. программа является макросами, необходимо снизить уровень безопасности приложения, для чего войти в основном меню по пути: Сервис > Макрос > Безопасность; на открывшейся вкладке выбрать средний уровень безопасности.
- Открыть файл программы и в открывшемся окне предупреждения системы безопасности выбрать «Не отключать макросы». Появится главное окно программы – «Данные».
Необходимо выбрать способ задания индуктивности входного контура (Lentr), отметив нужный вариант значком * в табличке справа. Обязательными данными являются: границы диапазона (Fmin, Fmax), собственная плюс монтажная ёмкость входного контура (Cm), минимальная и максимальная ёмкости КПЕ (Ctmin, Ctmax), тип настройки гетеродина в ячейке B25 (ввести слова «верхняя» или «нижняя», без кавычек) и значение промежуточной частоты (Fint) в ячейку B26.
Хотя программа довольно устойчива к начальным данным, надо иметь в виду, что выбираемые значения исходных величин не должны быть абсурдными. Например, это относится к частотам диапазона, который не должен быть чрезмерно широк, так что не может быть перекрыт выбранным КПЕ, равно и слишком узким, когда задача может стать вырожденной. Случай выбора варианта «Рассчитывается по Fmin,max (при отсутствии С1)» относится к нерастянутым диапазонам ДВ и СВ, а также к другим диапазонам, если используется КПЕ небольшой ёмкости. Обычно такой вариант надо выбирать, когда получаются очень большие значения C1 (более 10000 пФ) или меньше нуля. Если получаются отрицательными значения C2, это означает, что Cm велико для заданной Fmin. Возможны иные варианты ограничений, в которых пользователь может разобраться самостоятельно, действуя методом проб и ошибок.
Запускается программа нажатием <ctrl+s> при англоязычной раскладке клавиатуры. Программа заполняет все необходимые ячейки таблицы, за исключением трёх нижних (Надо иметь в виду, что до запуска программы в таблице остаются значения от предыдущих расчётов.). Следует внимательно ознакомиться с результатом и на появившемся сообщении «Готово» щёлкнуть «ОК». Откроется окно программы «МНК», где ничего, как правило, менять не нужно. Не следует также что-либо менять на служебных вкладках «Процесс» и «Параметры». Запустить второй этап вычислений следует нажатием <ctrl+f>. После щелчка на «ОК» в окошке «Готово» данные расчёта параметров гетеродинного контура заносятся в три последние строки листа «Данные». На этом вычисления заканчиваются.
VI. Примеры
1о. Рассмотрим расчёт сопряжения контуров для диапазона ДВ (0,145 – 0,415 мГц). Пусть имеется КПЕ от 12 до 495 пФ и входной контур с индуктивностью 2000 мкГн, собственная ёмкость, включая ёмкость монтажа равна 20 пФ. Значение ПЧ – 465 кГц, настройка гетеродина верхняя. Запускаем 1-ый макрос и получаем в результате С1 = - 6748,... В данном случае получилось С1<0 из-за того, что значение индуктивности мало, поэтому увеличим её до 2200. Новый результат С1 = 124371,... говорит о том, что надо выбрать вариант расчёта без C1. Переносим значок * в ячейку Е8 и получаем приемлемые параметры входного контура (округлённо): L = 2190 мкГн; С1 - отсутствует; С2 = 35,2 пФ. Запускаем 2-ой макрос и находим параметры контура гетеродина: L = 426 мкГн; С1 = 185 пФ; С2 = 71 пФ.
2о. Рассчитаем параметры контуров тракта 1-ой (перестраиваемой) ПЧ приёмника с двойным преобразованием частоты. Диапазон 1-ой ПЧ – 2,0-3,5 мГц. Индуктивность контуров селектора равна 27 мкГн. КПЕ от 25 до 446 пФ, собственная ёмкость 20 пФ, значение 2-ой ПЧ – 465 кГц, настройка гетеродина верхняя.
Результат в таблице:
|
Параметр |
Селектор |
Гетеродин |
|
индуктивность, мкГн |
27 |
21,0 |
|
С1, пФ |
383,23 |
279,58 |
|
С2, пФ |
41,39 |
46,19 |
Следует, конечно, иметь в виду, что после вычислений и пайки соответствующих схем всё равно так или иначе придётся корректировать найденные параметры, во-первых, потому, что собственные ёмкости катушек, монтажа и усилительных устройств не бывают точно известны, во-вторых, значения ёмкостей конденсаторов придётся округлять до ближайших с существующими номиналами и т.д. Однако предварительные расчёты сопряжения контуров по программе сильно облегчают их дальнейшую настройку.
С вопросами и замечаниями относительно метода расчёта и работы с программой можно обратиться к автору по эл. почте:
.
ЛИТЕРАТУРА
1. Левашов Ю.А. Приём и обработка сигналов.
4. Э. Бунин. Excel Visual Basic для приложений (серия «Без проблем!»): Пер. с англ. – М.: Восточная Книжная Компания, 1966. – 352 с.
Автор: Цибанов В.В.
Комментарии
Отзывы читателей - Скажите свое мнение!
Оставьте свое мнение
Авторизуйтесь, чтобы оставлять комментарии
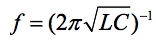
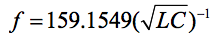
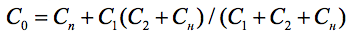
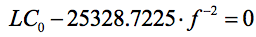
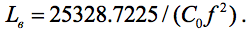
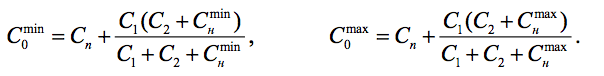
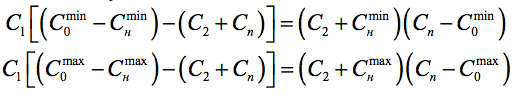
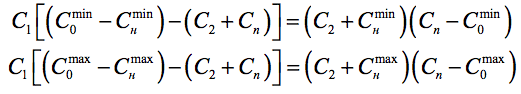
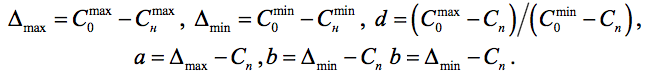
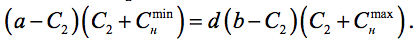
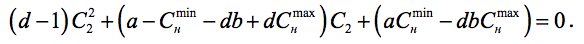
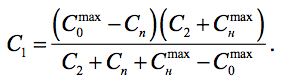
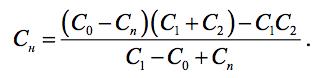 (5)
(5)